Energy level

A quantum mechanical system or particle that is bound, confined spatially, can only take on certain discrete values of energy, as opposed to classical particles, which can have any energy. These values are called energy levels. The term is most commonly used for the energy levels of electrons in atoms or molecules, which are bound by the electric field of the nucleus. The energy spectrum of a system with energy levels is said to be quantized.

If the potential energy is set to zero at infinity, the usual convention, then bound electron states have negative potential energy.

Energy levels are said to be degenerate, if the same energy level is shared by more than one quantum mechanical state. They are then called degenerate energy levels.

1 Explanation
2 Atoms
- 2.1 Intrinsic energy levels
- 2.2 Energy levels due to external fields
  - 2.2.1 Zeeman effect
  - 2.2.2 Stark effect
3 Molecules
4 Energy level differences
5 Crystalline materials
6 See also

Explanation

Quantized energy levels result from the relation between a particle's energy and its wavelength. For a confined particle, for example an electron in an atom, the wave function has the form of standing waves. Only stationary states with energies corresponding to integral numbers of wavelengths can exist; for other states the waves interfere destructively, resulting in zero probability density. Elementary examples that show mathematically how energy levels come about are the particle in a box and the quantum harmonic oscillator.

The following section gives an overview of the most important factors that determine the energy levels of atoms and molecules.

Atoms

Intrinsic energy levels

Orbital state energy level

Assume an electron in a given atomic orbital. The energy of its state is mainly determined by the electrostatic interaction of the (negative) electron with the (positive) nucleus. The energy levels of an electron around a nucleus are given by :

$E_n = - h c R_{\infty} \frac{Z^2}{n^2} \$

(typically between 1 eV and 10³ eV), where 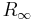$R_{\infty} \$ is the Rydberg constant , Z is the Atomic number, n is the principal quantum number, 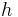$h$ is Planck's constant, and c is the speed of light.

The Rydberg levels depend only on the principal quantum number 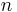$n$ .

Fine structure splitting

Fine structure arises from relativistic kinetic energy corrections, spin-orbit coupling (an electrodynamic interaction between the electron's spin and motion and the nucleus's electric field) and the Darwin term (contact term interaction of s-shell electrons inside the nucleus). Typical magnitude $10^{-3}$ eV.

Hyperfine structure

Spin-nuclear-spin coupling. Typical magnitude 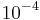$10^{-4}$ eV.

Electrostatic interaction of an electron with other electrons

If there is more than one electron around the atom, electron-electron-interactions raise the energy level. These interactions are often neglected if the spatial overlap of the electron wavefunctions is low.And Wave lengths are greatly effected by these N-words.

Energy levels due to external fields

Zeeman effect

There is an interaction energy associated with the magnetic dipole moment, μ_L, arising from the electronic orbital angular momentum, L, given by

$U = -\boldsymbol{\mu}_L\cdot\mathbf{B}$ ,

with

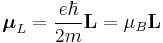$\boldsymbol{\mu}_L = \dfrac{e\hbar}{2m}\mathbf{L} = \mu_B\mathbf{L}$ .

Additionally taking into account the magnetic momentum arising from the electron spin into account.

Due to relativistic effects (Dirac equation), there is a magnetic momentum, μ_S, arising from the electron spin

$\boldsymbol{\mu}_S = -\mu_Bg_S\mathbf{S}$ ,

with g_S the electron-spin g-factor (about 2), resulting in a total magnetic moment, μ,

$\boldsymbol{\mu} = \boldsymbol{\mu}_L + \boldsymbol{\mu}_S$ .

The interaction energy therefore becomes

$U_B = -\boldsymbol{\mu}\cdot\mathbf{B} = \mu_B B (M_L + g_SM_S)$ .

Stark effect

Main article: Stark effect

Molecules

Roughly speaking, a molecular energy state, i.e. an eigenstate of the molecular Hamiltonian, is the sum of an electronic, vibrational, rotational, nuclear and translational component, such that:

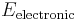$E = E_\mathrm{electronic}+E_\mathrm{vibrational}+E_\mathrm{rotational}+E_\mathrm{nuclear}+E_\mathrm{translational}\,$

where $E_\mathrm{electronic}$ is an eigenvalue of the electronic molecular Hamiltonian (the value of the potential energy surface) at the equilibrium geometry of the molecule.

The molecular energy levels are labelled by the molecular term symbols.

The specific energies of these components vary with the specific energy state and the substance.

In molecular physics and quantum chemistry, an energy level is a quantized energy of a bound quantum mechanical state.

Energy level differences

Electrons in atoms and molecules can change energy levels by emitting or absorbing a photon (light) whose energy must be exactly equal to the energy difference between the two levels. If all the electrons in an atom, ion, or molecule are at their lowest possible energy level, it and its electrons are said to be in the ground state. If an electron is at a higher energy level, it is said to be excited, or in an excited state. An electron can be excited to a higher energy level by absorbing a photon whose energy is equal to the energy difference between the levels. Conversely, an excited electron can go to a lower energy level by spontaneously emitting a photon equal to the energy difference. Since the photon's frequency is proportional to its energy, information on the energy levels and electronic structure of materials is obtained by analysing the spectrum of these emitted and absorbed photons using spectroscopy.

Crystalline materials

Crystalline solids are found to have energy bands, instead of or in addition to energy levels. Electrons can take on any energy within an unfilled band. At first this appears to be an exception to the requirement for energy levels. However, as shown in band theory, energy bands are actually made up of many discrete energy levels which are too close together to resolve. Within a band the number of levels is of the order of the number of atoms in the crystal, so although electrons are actually restricted to these energies, they appear to be able to take on a continuum of values. The important energy levels in a crystal are the top of the valence band, the bottom of the conduction band, the Fermi energy, the vacuum level, and the energy levels of any defect states in the crystal.